Adding Inferential Information to Plots
using Resampling and Animations

Abstract

We present a method for adding inferential information to arbitrary statistical plots based on resampling and animation. A large number of bootstrap datasets are created and subjected to the same analyses and plotting procedures than the original dataset. These "bootstrap plots" are then animated to reveal the statistical noise that was hidden in the original plot, in order to help readers appreciate the uncertainty in the quantities, trends and patterns conveyed by the plot. We illustrate this approach with a real study taken from the information visualization literature.

Author Keywords

Multiverse analysis; statistical dance.

ACM Classification Keywords

H5.2 User Interfaces: Evaluation/Methodology

General Terms

Human Factors; Design; Experimentation; Measurement.

Introduction

It is well known that results from statistical analyses should always be presented with inferential information in order to prevent misinterpretation. This is the case not only for numbers but also for plots. For example, point estimates should always be presented together with a graphical indication of their uncertainty, such as error bars for interval estimates or density plots for posterior distributions . However, it can be challenging to present inferential information when a plot is very dense or when it involves visual representations for which there is no known method for conveying inferential information. For example, when showing a ranking of different conditions, it is not clear at all how can inferential information be conveyed. Yet, without inferential information uncertainty remains hidden. Here, we suggest a general solution based on resampling and animation. We illustrate it by reproducing the figures from a study by Harrison et al. .

Background

Statistical dances

The term statistical dance has been used to refer to a plot or an animation that shows the outcomes of multiple simulated replications of the same hypothetical experiment . This term originates from Geoff Cumming's "dance of p-values", a simple simulation that was meant to show how widely p-values vary across replications . The simulation consisted in repeatedly drawing a sample from two normal distributions and computing the p-value for the difference in means. A dance of 95% confidence intervals was also shown. This idea was later applied to Bayes factors and to a range of other statistics .

Statistical dances are a particular case hypothetical outcome plots (HOPs) , that "visualize a set of draws from a distribution, where each draw is shown as a new plot in either a small multiples or animated form".

Here we show that statistical dances can be applied not only to simulations where the population is known, but also to existing datasets where the population is unknown. This is possible thanks to resampling methods.

Resampling

Resampling refers to a family of statistical methods where a range of alternative datasets are constructed from a real dataset in order to answer statistical questions. A common approach, called nonparametric bootstrapping, consists of constructing many alternative samples (called bootstrap samples) by randomly drawing same-size samples with replacement . The distribution of a statistic (e.g, the sample mean) computed on a large set of bootstrap samples is called the statistic's bootstrap distribution. In many cases, the bootstrap distribution provides a good approximation of the sampling distribution , making it possible to derive approximate confidence intervals without parametric assumptions .

Here we use bootstrapping not for deriving confidence intervals, but for constructing a set of alternative datasets based on an original (real) dataset. Each dataset is subjected to the same analysis and plotting procedure, yielding a set of bootstrap plots. Once animated, the bootstrap plots become a statistical dance that can convey useful information on the reliability of the different quantities, trends and patterns depicted by the plot. In the next section we illustrate this with concrete examples.

Example

We chose the study by Harrison et al. because the data and analysis scripts are publicly available, and because the article contains an interesting assortment of plots, including a ranking plot. We first briefly summarize the study.

Harrison et al.'s Study

The goal of the study was to rank nine existing visualizations in their ability to effectively convey correlations. We focus on experiment 2, which was the main experiment and for which data and analysis code are available. In that experiment, nine visualizations were evaluated on 1,600+ crowdsourcing workers on their ability to convey correlation. The staircase method was used to derive just-noticeable difference (JND) values, which capture discrimination capacity: the lower the value, the better the participant can discriminate between correlations.

The experiment involved four independent variables: the visualization type (9 levels), the base correlation value (6 levels), whether the correlation was positive or negative (2 levels), and whether the value was approached from above or from below (2 levels). Each participant carried out 4 tasks, each with a specific combination of conditions.

Bootstrapping the dataset

The experimental dataset and analysis scripts from Harrison et al. are available at github.com/TuftsVALT/ranking-correlation. The dependent variable is JND. Again, each participant contributed four JND values, corresponding to four different combinations of conditions. The dataset has data from 1693 participants, and thus a total of 1693×4 = 6772 JND values. Since the experiment involves 9×6×2×2 = 216 unique conditions, each unique condition was tested multiple times, on different participants (31.4 times on average, min=21, max=41). We generate a bootstrap dataset by independently bootstrapping (resampling with replacement) each of these 216 subsamples. We ignored participant ID since it is not used in any of the models in the reported analysis (we verified that shuffling the participant ID column led to the exact same plots). The bootstrap dataset is then saved in a csv file and fed to the same analysis scripts, producing a new set of plots. This procedure was repeated 100 times.

Results

All the plots in this section are:

• Plots computed from the original dataset, as initially reported by Harrison et al. .
• Plots computed from the bootstrap dataset #. Press and hold the Animate multiverse button on top or the "A" key to animate.

We report the plots in the same order as in the original article. Figure 1 (Figure 4 in the original paper) shows the mean JND for each of the 216 conditions, each displayed as a dot. Here inferential information is already conveyed by the way of error bars, so the dance is somewhat redundant. However, showing the dance still has educational value, as researchers tend to grossly overestimate the reliability and the replicability of inferential statistics such as p-values and confidence intervals . One might notice that the error bars are jumping more wildly than in a regular dance of 95% confidence intervals . This is because the error bars are standard errors, which are approximately twice as short as 95% CIs. Although in the original article this was clearly stated in the Figure caption, the dance might make it less likely for the reader to miss this important information.

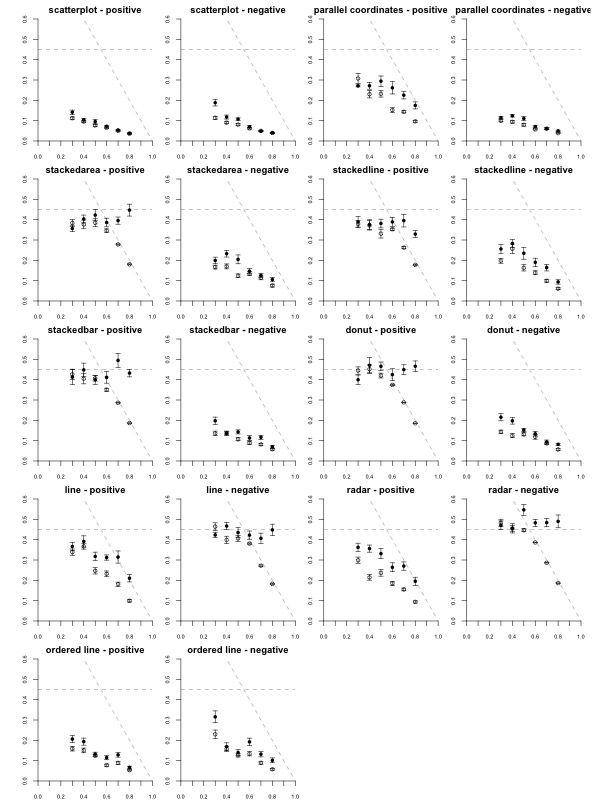
Figure 1 provides lots of details about the data but is also somehow overwhelming. Thus it was only used for i) informally confirming the approximately linear relationship between R and JND; and ii) showing that both visualization and correlation sign can have a strong effect on overall performance (e.g., compare stackedbar positive vs. stackedbar negative); iii) showing that some visualization × sign conditions often perform below chance level (JND > 0.45 -- these conditions are removed from the rest of the analysis). These informal observations appear to hold reasonably well across bootstrap datasets.

Figure 2 (Figure 5 in the original paper) shows linear regression results for several pairs of visualization techniques. The lower a line the better the performance. Some differences are large and extremely consistent across bootstrap datasets: for example, the inferiority of line-positive over the two other conditions on the first plot, or the inferiority of parallel-coordinates-positive on the last plot. Other differences are less clear but actually hold in a vast majority of bootstrap datasets: for example, the overall superiority of radar-positive in the second plot and of stackedbar-negative in the third plot. In contrast, many other comparisons are inconclusive. All these informal inferences agree with formal null hypothesis significance tests reported in the original paper. Although formal tests inspire more confidence to many readers, interpreting them together with effect size figures requires constant back and forth between figures and p-values provided in the text or in a table. Doing so is often quite tedious and can easily cause impatient readers to give up and be content with a superficial examination of the results.

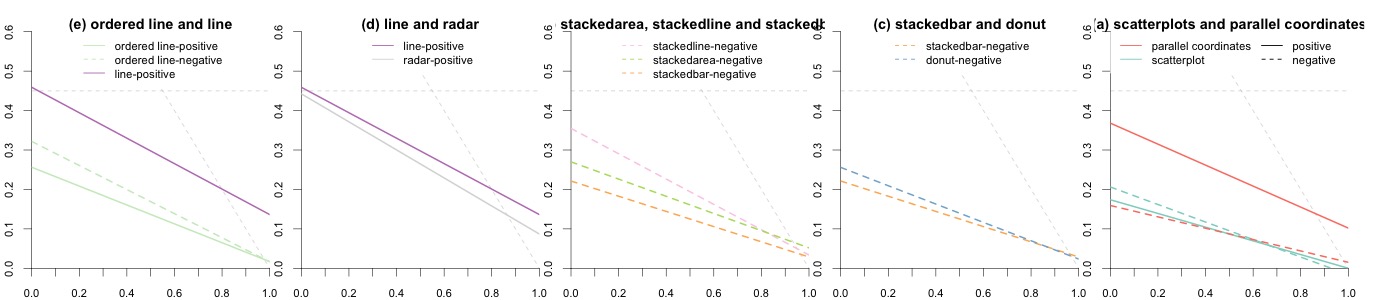
It is possible — and common practice — to display a 95% confidence interval around a regression line by plotting a confidence limit curve on each side of the line. Such visual representations can greatly facilitate inference but can also easily produce cluttered plots. Although it may have been possible to add 95% confidence intervals to Figure 2, doing so with Figure 3 would have likely rendered it illegible.

Figure 3 (Figure 6 in the original paper) shows the regression lines for all conditions, as well as the results from a previous similar experiment . The figure is consistent with the paper's main findings: "using scatterplots to depict correlation results in better performance overall. However, this performance difference only occurs when depicting positively correlated data. In fact, parallel coordinates depicting negatively correlated data appear to perform as well as scatterplots" . The statistical dance gives credence to these conclusions, while at the same time providing a faithful illustration of the uncertainty behind the estimates. The reader is free to linger on the figure and go beyond the authors's own summary of findings by examining other comparisons and drawing their own conclusions. All necessary information on effect sizes and inferential statistics is seamlessly combined into this single animated figure, and it would take pages and pages of text to fully describe it.

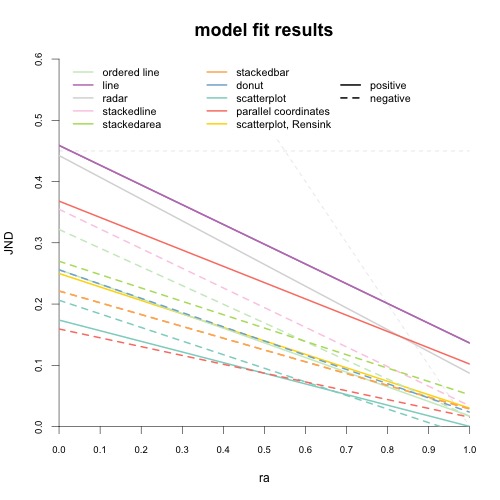
Figure 4 (Figure 7 in the original paper) shows the ranking of visualizations depending on whether they are used to convey negative (-neg suffix) or positive (-pos suffix) correlations. A ranking is provided for different correlation values (r), and overall (right column). Here animation becomes crucial because this chart provides an easy-to-process summary of the paper's results, thus many readers may feel they can skip the gory details and get their take-home message from this chart only. However, as a still figure, the chart does not include inferential information and thus does not convey uncertainty.

The statistical dance of Figure 4 reveals an intermixing of reliable trends and statistical noise. A reliable trend, for example, is that parallel coordinates applied to negative correlations (pcp-neg) loses some its advantages as correlations approach -1. Looking at the overall ranking in the right column, one can also be very confident that line is the worst technique for positive correlations, followed by radar and then by pcp. As for the top of the list, the scatterplot is clearly better at conveying positive correlations than negative correlations, but it is likely that pcp beats the scatterplot at negative correlations. Around the middle of the ranking there is a lot of noise, so it is probably hard to come up with a reliable absolute ranking.

It is useful to ask what changes to Figure 4 would have made the chart less "jumpy". One option could have been to show partial orderings with ties rather than total orderings. Alternatively, one may focus on showing relative performances on a continuous scale rather than discrete rankings. In fact, it has been suggested that statistical charts should ideally be designed to be smooth functions of the data because this makes them more robust to sampling variability . Thus, statistical dances are useful not only because they can reveal uncertainty to readers, but also because they can reveal uncertainty to authors and encourage them to design charts that are as stable -- and hence as trustworthy -- as possible.

Discussion and Conclusion

It is important to understand that the statistical dances shown here are not exact in that they do not show an accurate sequence of replications as in simulation-based dances . If the dances were exact, then we would be able to derive exact population parameters by aggregating all simulated replications, which is of course impossible. Creating an exact dance requires knowledge of the true sampling distributions, and thus knowledge of the real population parameters (or model). Instead, the dances shown here are best guesses of what real replications would look like if the same experiment was to be replicated over and over again. These best guesses rely on the properties of bootstrapping, a simple but well-established and powerful statistical inference tool.

Though they are only approximations, animated bootstrap plots convey useful inferential information that allows readers to appreciate to what extent different values, trends and patterns shown in the plots are robust and reliable. Dances can act as substitutes for static displays of inferential information when these cannot be easily visualized. They can also usefully complement inferential plots by dispelling the common misconception that a perfectly-executed inferential analysis is fully reliable and will give the same or similar results if the experiment is to be replicated . Though the approach is general and can be applied to virtually any plot, the dataset bootstrapping procedure requires a case-by-case treatement as it depends on the structure of the dataset and on the performed analyses. Not all datasets may be bootstrappable.

We focused on using sequential animations, a common approach for communicating uncertainty. Statistical dances can also be represented in a static manner by stacking all outcomes (see, e.g., Figure 7 in ). However, this approach may not generalize well to complex 2D plots. Another alternative could be to compose multiple plots using alpha-blending or overplotting.